The Elevator Accelerates Upward Momentarily at the Rate of 2 M/s2. What Does the Scale Read Then?

half-dozen Applications of Newton's Laws

vi.one Solving Problems with Newton's Laws

Learning Objectives

By the cease of the section, you will exist able to:

• Employ trouble-solving techniques to solve for quantities in more complex systems of forces
• Utilise concepts from kinematics to solve bug using Newton's laws of motion
• Solve more than complex equilibrium problems
• Solve more circuitous acceleration problems
• Apply calculus to more advanced dynamics bug

Success in problem solving is necessary to sympathise and use physical principles. We developed a design of analyzing and setting upwards the solutions to bug involving Newton'due south laws in Newton's Laws of Motion; in this chapter, we go on to hash out these strategies and utilise a step-by-pace process.

Trouble-Solving Strategies

We follow here the basics of problem solving presented earlier in this text, only we emphasize specific strategies that are useful in applying Newton's laws of motion . In one case you identify the physical principles involved in the problem and determine that they include Newton'southward laws of motion, you can apply these steps to detect a solution. These techniques too reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, and then the following techniques should reinforce skills you take already begun to develop.

Problem-Solving Strategy: Applying Newton'southward Laws of Motion

1. Identify the physical principles involved by listing the givens and the quantities to be calculated.
2. Sketch the situation, using arrows to represent all forces.
3. Make up one's mind the system of interest. The result is a free-torso diagram that is essential to solving the problem.
4. Employ Newton'due south 2d law to solve the problem. If necessary, apply appropriate kinematic equations from the affiliate on move along a straight line.
5. Check the solution to see whether it is reasonable.

Let'south use this problem-solving strategy to the challenge of lifting a grand pianoforte into a second-story apartment. Once we have determined that Newton's laws of motion are involved (if the problem involves forces), it is peculiarly important to draw a conscientious sketch of the situation. Such a sketch is shown in (Figure)(a). And so, as in (Effigy)(b), we tin can represent all forces with arrows. Whenever sufficient information exists, it is best to label these arrows carefully and make the length and direction of each correspond to the represented force.

Figure 6.2 (a) A grand piano is being lifted to a second-story flat. (b) Arrows are used to represent all forces:

is the tension in the rope higher up the piano,

is the force that the piano exerts on the rope, and

is the weight of the piano. All other forces, such as the nudge of a breeze, are assumed to exist negligible. (c) Suppose we are given the piano'southward mass and asked to observe the tension in the rope. We then define the system of interest equally shown and depict a costless-body diagram. At present

is no longer shown, because it is not a forcefulness acting on the system of interest; rather,

acts on the outside world. (d) Showing only the arrows, the head-to-tail method of addition is used. It is apparent that if the pianoforte is stationary,

.

Every bit with most problems, nosotros next need to identify what needs to be adamant and what is known or tin can be inferred from the problem as stated, that is, make a list of knowns and unknowns. Information technology is particularly crucial to identify the system of interest, since Newton's second law involves only external forces. We tin then determine which forces are external and which are internal, a necessary step to utilize Newton'south second law. (See (Effigy)(c).) Newton'due south third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated in Newton's Laws of Motility, the arrangement of involvement depends on the question we need to answer. Only forces are shown in costless-body diagrams, not acceleration or velocity. We have drawn several costless-trunk diagrams in previous worked examples. (Figure)(c) shows a free-trunk diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Once a free-body diagram is fatigued, we apply Newton's 2d police. This is washed in (Figure)(d) for a particular situation. In general, once external forces are clearly identified in complimentary-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, every bit done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then the forces can be handled algebraically. If the problem is two-dimensional, then it must be cleaved downwards into a pair of i-dimensional problems. Nosotros do this past projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with ane axis parallel to the incline and one perpendicular to information technology is well-nigh convenient. Information technology is almost always convenient to make i axis parallel to the direction of move, if this is known. Generally, just write Newton's 2nd constabulary in components along the unlike directions. Then, you lot have the following equations:

(If, for instance, the system is accelerating horizontally, then you tin can and then prepare

) We need this information to determine unknown forces acting on a system.

Equally always, we must bank check the solution. In some cases, it is piece of cake to tell whether the solution is reasonable. For instance, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving; with experience, it becomes progressively easier to judge whether an respond is reasonable. Another way to check a solution is to check the units. If we are solving for force and stop upwardly with units of millimeters per second, then nosotros have made a mistake.

There are many interesting applications of Newton's laws of motion, a few more of which are presented in this section. These serve also to illustrate some further subtleties of physics and to assist build problem-solving skills. We wait start at problems involving particle equilibrium, which make use of Newton'southward beginning law, and then consider particle acceleration, which involves Newton's second law.

Particle Equilibrium

Recall that a particle in equilibrium is 1 for which the external forces are balanced. Static equilibrium involves objects at remainder, and dynamic equilibrium involves objects in motion without acceleration, but it is important to remember that these atmospheric condition are relative. For instance, an object may be at rest when viewed from our frame of reference, simply the aforementioned object would appear to exist in motion when viewed past someone moving at a constant velocity. We now make utilize of the noesis attained in Newton's Laws of Motion, regarding the different types of forces and the use of free-torso diagrams, to solve additional issues in particle equilibrium .

Case

Different Tensions at Different Angles

Consider the traffic low-cal (mass of 15.0 kg) suspended from two wires as shown in (Figure). Find the tension in each wire, neglecting the masses of the wires.

Figure 6.3 A traffic calorie-free is suspended from two wires. (b) Some of the forces involved. (c) Only forces acting on the system are shown here. The free-torso diagram for the traffic light is also shown. (d) The forces projected onto vertical (y) and horizontal (ten) axes. The horizontal components of the tensions must abolish, and the sum of the vertical components of the tensions must equal the weight of the traffic light. (east) The free-torso diagram shows the vertical and horizontal forces acting on the traffic lite.

Strategy

The system of interest is the traffic low-cal, and its costless-body diagram is shown in (Figure)(c). The three forces involved are not parallel, and so they must be projected onto a coordinate system. The most convenient coordinate system has ane axis vertical and i horizontal, and the vector projections on it are shown in (Effigy)(d). There are two unknowns in this problem (

and

), and so two equations are needed to find them. These two equations come up from applying Newton's second law along the vertical and horizontal axes, noting that the net external force is zero forth each axis because dispatch is zip.

Solution

First consider the horizontal or x-axis:

Thus, every bit you might wait,

This gives us the following human relationship:

Thus,

Note that

and

are not equal in this case because the angles on either side are not equal. It is reasonable that

ends up being greater than

because it is exerted more vertically than

Now consider the force components along the vertical or y-axis:

This implies

Substituting the expressions for the vertical components gives

In that location are two unknowns in this equation, but substituting the expression for

in terms of

reduces this to one equation with i unknown:

which yields

Solving this final equation gives the magnitude of

to be

Finally, we find the magnitude of

by using the relationship betwixt them,

, constitute above. Thus we obtain

Significance

Both tensions would be larger if both wires were more horizontal, and they volition be equal if and only if the angles on either side are the aforementioned (as they were in the earlier example of a tightrope walker in Newton's Laws of Motion.

Particle Acceleration

We accept given a variety of examples of particles in equilibrium. We now plow our attending to particle acceleration problems, which are the result of a nonzero cyberspace force. Refer again to the steps given at the beginning of this department, and notice how they are practical to the following examples.

Example

Drag Force on a Barge

Two tugboats push on a clomp at different angles ((Figure)). The first tugboat exerts a force of

in the 10-direction, and the second tugboat exerts a force of

in the y-direction. The mass of the barge is

and its acceleration is observed to be

in the direction shown. What is the drag strength of the water on the clomp resisting the motion? (Note: Drag forcefulness is a frictional strength exerted by fluids, such equally air or h2o. The elevate force opposes the motility of the object. Since the barge is apartment bottomed, we can presume that the elevate force is in the direction opposite of motion of the clomp.)

Figure six.4 (a) A view from above of 2 tugboats pushing on a barge. (b) The free-body diagram for the transport contains simply forces acting in the aeroplane of the h2o. It omits the two vertical forces—the weight of the clomp and the buoyant force of the h2o supporting it cancel and are not shown. Note that

is the total applied force of the tugboats.

Strategy

The directions and magnitudes of acceleration and the applied forces are given in (Figure)(a). We ascertain the total force of the tugboats on the barge equally

so that

The elevate of the water

is in the direction contrary to the management of motion of the boat; this strength thus works against

equally shown in the gratuitous-body diagram in (Figure)(b). The system of involvement here is the barge, since the forces on it are given also as its acceleration. Because the applied forces are perpendicular, the ten– and y-axes are in the same management as

and

The problem quickly becomes a one-dimensional problem forth the management of

, since friction is in the direction opposite to

Our strategy is to notice the magnitude and direction of the net practical forcefulness

and then utilise Newton's second law to solve for the drag force

Solution

Since

and

are perpendicular, nosotros tin observe the magnitude and direction of

direct. First, the resultant magnitude is given by the Pythagorean theorem:

The angle is given by

From Newton'due south first law, nosotros know this is the same direction as the acceleration. Nosotros also know that

is in the contrary direction of

since information technology acts to slow downwards the acceleration. Therefore, the net external force is in the aforementioned management as

but its magnitude is slightly less than

The trouble is at present 1-dimensional. From the complimentary-body diagram, we can see that

However, Newton'south second law states that

Thus,

This tin can be solved for the magnitude of the elevate force of the water

in terms of known quantities:

Substituting known values gives

The direction of

has already been determined to exist in the direction opposite to

or at an angle of

due south of w.

Significance

The numbers used in this example are reasonable for a moderately large barge. It is certainly hard to obtain larger accelerations with tugboats, and pocket-size speeds are desirable to avoid running the barge into the docks. Drag is relatively small for a well-designed hull at low speeds, consistent with the answer to this example, where

is less than 1/600th of the weight of the ship.

In Newton'due south Laws of Move, we discussed the normal force , which is a contact forcefulness that acts normal to the surface then that an object does not take an acceleration perpendicular to the surface. The bathroom scale is an excellent example of a normal forcefulness acting on a torso. Information technology provides a quantitative reading of how much it must button upward to support the weight of an object. Just can you predict what y'all would see on the dial of a bath calibration if you stood on it during an elevator ride? Will y'all see a value greater than your weight when the elevator starts upwards? What near when the elevator moves upward at a constant speed? Take a guess earlier reading the next example.

Instance

What Does the Bathroom Scale Read in an Elevator?(Figure) shows a 75.0-kg human being (weight of about 165 lb.) standing on a bath scale in an lift. Calculate the scale reading: (a) if the elevator accelerates upward at a rate of

and (b) if the lift moves up at a constant speed of 1 m/southward.

Effigy 6.5 (a) The various forces acting when a person stands on a bathroom scale in an elevator. The arrows are approximately correct for when the lift is accelerating upwardly—broken arrows represent forces too large to be fatigued to scale.

is the tension in the supporting cable,

is the weight of the person,

is the weight of the calibration,

is the weight of the elevator,

is the forcefulness of the scale on the person,

is the force of the person on the scale,

is the force of the scale on the floor of the elevator, and

is the force of the floor upward on the scale. (b) The complimentary-trunk diagram shows simply the external forces acting on the designated system of interest—the person—and is the diagram we use for the solution of the problem.

Strategy

If the scale at rest is accurate, its reading equals

, the magnitude of the forcefulness the person exerts down on it. (Figure)(a) shows the numerous forces acting on the elevator, calibration, and person. Information technology makes this i-dimensional trouble look much more than formidable than if the person is chosen to be the system of interest and a free-trunk diagram is drawn, as in (Figure)(b). Assay of the free-body diagram using Newton'southward laws can produce answers to both (Figure)(a) and (b) of this example, equally well as some other questions that might arise. The only forces interim on the person are his weight

and the upward force of the calibration

According to Newton'due south 3rd law,

and

are equal in magnitude and opposite in direction, so that we need to find

in order to find what the scale reads. We tin can do this, as usual, by applying Newton'southward second law,

From the complimentary-torso diagram, we see that

so we have

Solving for

gives us an equation with simply one unknown:

or, because

just

No assumptions were fabricated about the acceleration, so this solution should be valid for a multifariousness of accelerations in addition to those in this situation. (Note: We are considering the case when the elevator is accelerating upward. If the elevator is accelerating downward, Newton's second police becomes

)

Solution

1. We accept

   

   and so that

   

   yielding

   

2. Now, what happens when the elevator reaches a constant upward velocity? Will the scale still read more his weight? For any abiding velocity—up, down, or stationary—acceleration is zilch because

   

   and

   

   Thus,

   

   or

   

   which gives

   

Significance

The calibration reading in (Effigy)(a) is near 185 lb. What would the scale take read if he were stationary? Since his dispatch would be nothing, the force of the calibration would be equal to his weight:

Thus, the scale reading in the elevator is greater than his 735-N (165-lb.) weight. This means that the scale is pushing up on the person with a force greater than his weight, as it must in order to advance him upward. Clearly, the greater the acceleration of the elevator, the greater the calibration reading, consistent with what you feel in chop-chop accelerating versus slowly accelerating elevators. In (Effigy)(b), the scale reading is 735 N, which equals the person'southward weight. This is the instance whenever the lift has a constant velocity—moving up, moving downwardly, or stationary.

Check Your Understanding

Now calculate the calibration reading when the elevator accelerates downward at a rate of

[reveal-reply q="fs-id1165037222074″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1165037222074″]

[/hidden-answer]

The solution to the previous example besides applies to an elevator accelerating downward, every bit mentioned. When an elevator accelerates downward, a is negative, and the calibration reading is less than the weight of the person. If a constant downward velocity is reached, the scale reading again becomes equal to the person's weight. If the elevator is in free fall and accelerating downward at thou, then the calibration reading is goose egg and the person appears to be weightless.

Example

Two Attached Blocks(Figure) shows a cake of mass

on a frictionless, horizontal surface. It is pulled by a light string that passes over a frictionless and massless pulley. The other end of the string is connected to a block of mass

Discover the dispatch of the blocks and the tension in the string in terms of

Figure 6.6 (a) Block 1 is connected by a light string to block ii. (b) The free-body diagrams of the blocks.

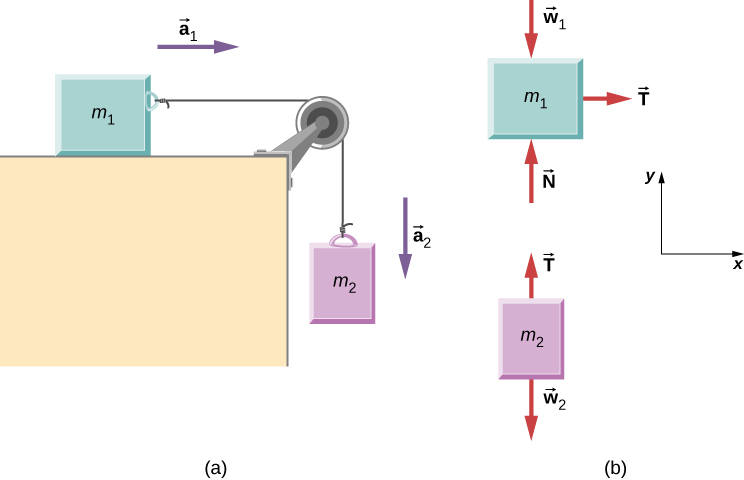
Strategy

We draw a free-body diagram for each mass separately, as shown in (Effigy). Then nosotros clarify each i to notice the required unknowns. The forces on block i are the gravitational force, the contact force of the surface, and the tension in the string. Cake ii is subjected to the gravitational force and the cord tension. Newton's second constabulary applies to each, so we write ii vector equations:

For block one:

For cake two:

Notice that

is the same for both blocks. Since the string and the pulley have negligible mass, and since there is no friction in the caster, the tension is the same throughout the string. We can now write component equations for each block. All forces are either horizontal or vertical, then we can utilise the aforementioned horizontal/vertical coordinate arrangement for both objects

Solution

The component equations follow from the vector equations above. We see that cake 1 has the vertical forces balanced, so we ignore them and write an equation relating the ten-components. In that location are no horizontal forces on block ii, and then simply the y-equation is written. We obtain these results:

When cake i moves to the right, block 2 travels an equal distance downward; thus,

Writing the common acceleration of the blocks as

nosotros now have

and

From these two equations, we can express a and T in terms of the masses

and

Significance

Find that the tension in the string is less than the weight of the block hanging from the terminate of it. A common error in bug similar this is to fix

You can see from the free-body diagram of block 2 that cannot be correct if the block is accelerating.

Bank check Your Understanding

Summate the acceleration of the organisation, and the tension in the string, when the masses are

and

[reveal-answer q="fs-id1165036742049″]Show Solution[/reveal-answer]

[subconscious-respond a="fs-id1165036742049″]

[/subconscious-answer]

Example

Atwood Automobile

A classic problem in physics, like to the one we but solved, is that of the Atwood motorcar , which consists of a rope running over a pulley, with two objects of dissimilar mass attached. Information technology is particularly useful in understanding the connection between strength and motion. In (Figure),

and

Consider the caster to exist frictionless. (a) If

is released, what will its dispatch be? (b) What is the tension in the string?

Figure 6.7 An Atwood machine and free-torso diagrams for each of the 2 blocks.

Strategy

We draw a free-body diagram for each mass separately, every bit shown in the figure. Then nosotros clarify each diagram to find the required unknowns. This may involve the solution of simultaneous equations. Information technology is also important to note the similarity with the previous example. As block two accelerates with acceleration

in the downward direction, block 1 accelerates upward with acceleration

. Thus,

Solution

1. We have

   

   (The negative sign in front end of

   

   indicates that

   

   accelerates downward; both blocks accelerate at the aforementioned rate, simply in reverse directions.) Solve the 2 equations simultaneously (subtract them) and the result is

   

   Solving for a:

   

2. Observing the first block, we see that

   

Significance

The result for the dispatch given in the solution can exist interpreted as the ratio of the unbalanced force on the system,

, to the full mass of the system,

. We tin can besides use the Atwood machine to measure local gravitational field force.

Check Your Understanding

Determine a general formula in terms of

and g for computing the tension in the string for the Atwood motorcar shown to a higher place.

[reveal-answer q="fs-id1165037181504″]Show Solution[/reveal-answer]

[hidden-respond a="fs-id1165037181504″]

(This is establish by substituting the equation for acceleration in (Effigy)(a), into the equation for tension in (Effigy)(b).)
[/hidden-answer]

Newton'southward Laws of Motility and Kinematics

Physics is most interesting and most powerful when applied to general situations that involve more than than a narrow gear up of concrete principles. Newton'south laws of motion can likewise be integrated with other concepts that have been discussed previously in this text to solve bug of motion. For case, forces produce accelerations, a topic of kinematics , and hence the relevance of earlier chapters.

When approaching problems that involve various types of forces, dispatch, velocity, and/or position, listing the givens and the quantities to exist calculated will allow you to place the principles involved. Then, you can refer to the chapters that deal with a particular topic and solve the problem using strategies outlined in the text. The following worked example illustrates how the trouble-solving strategy given earlier in this chapter, likewise equally strategies presented in other chapters, is applied to an integrated concept problem.

Example

What Force Must a Soccer Player Exert to Accomplish Top Speed?

A soccer player starts at rest and accelerates forward, reaching a velocity of 8.00 m/s in 2.50 southward. (a) What is her average acceleration? (b) What boilerplate force does the ground exert frontwards on the runner then that she achieves this acceleration? The actor'south mass is seventy.0 kg, and air resistance is negligible.

Strategy

To find the answers to this trouble, we employ the problem-solving strategy given earlier in this chapter. The solutions to each part of the instance illustrate how to apply specific trouble-solving steps. In this example, we do not need to utilize all of the steps. We but identify the physical principles, and thus the knowns and unknowns; use Newton'due south second law; and check to see whether the answer is reasonable.

Solution

1. We are given the initial and concluding velocities (goose egg and 8.00 m/due south forward); thus, the change in velocity is

   

   . We are given the elapsed time, and then

   

   The unknown is dispatch, which tin can be found from its definition:

   

   Substituting the known values yields

   

2. Here we are asked to notice the average force the ground exerts on the runner to produce this acceleration. (Remember that nosotros are dealing with the forcefulness or forces acting on the object of interest.) This is the reaction forcefulness to that exerted by the player astern confronting the ground, by Newton's 3rd law. Neglecting air resistance, this would exist equal in magnitude to the cyberspace external strength on the player, since this force causes her dispatch. Since we now know the player'southward acceleration and are given her mass, we can use Newton's second law to find the strength exerted. That is,

   

   Substituting the known values of grand and a gives

   

This is a reasonable event: The dispatch is attainable for an athlete in good condition. The force is about 50 pounds, a reasonable average force.

Significance

This example illustrates how to apply problem-solving strategies to situations that include topics from different chapters. The first step is to place the physical principles, the knowns, and the unknowns involved in the problem. The second stride is to solve for the unknown, in this example using Newton's second police. Finally, we check our answer to ensure information technology is reasonable. These techniques for integrated concept problems will be useful in applications of physics outside of a physics grade, such as in your profession, in other science disciplines, and in everyday life.

Check Your Agreement

The soccer player stops later on completing the play described above, but at present notices that the brawl is in position to be stolen. If she now experiences a force of 126 Due north to attempt to steal the ball, which is two.00 m away from her, how long will it take her to get to the ball?

[reveal-answer q="fs-id1165036851735″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1165036851735″]

1.49 south

[/hidden-respond]

Example

What Force Acts on a Model Helicopter?

A 1.50-kg model helicopter has a velocity of

at

It is accelerated at a constant rate for two seconds (2.00 s) after which it has a velocity of

What is the magnitude of the resultant force interim on the helicopter during this time interval?

Strategy

We can easily gear up up a coordinate system in which the ten-centrality

direction) is horizontal, and the y-axis

management) is vertical. We know that

and

From this, nosotros can calculate the acceleration past the definition; we can and so apply Newton's second law.

Solution

Nosotros have

The magnitude of the force is at present easily found:

Significance

The original problem was stated in terms of

vector components, so we used vector methods. Compare this case with the previous example.

Check Your Understanding

Observe the direction of the resultant for the 1.l-kg model helicopter.

[reveal-answer q="fs-id1165036738261″]Show Solution[/reveal-answer]

[subconscious-answer a="fs-id1165036738261″]

49.4 degrees

[/hidden-reply]

Example

Baggage Tractor(Effigy)(a) shows a baggage tractor pulling luggage carts from an plane. The tractor has mass 650.0 kg, while cart A has mass 250.0 kg and cart B has mass 150.0 kg. The driving forcefulness acting for a cursory catamenia of fourth dimension accelerates the arrangement from rest and acts for 3.00 s. (a) If this driving force is given by

observe the speed after three.00 seconds. (b) What is the horizontal strength acting on the connecting cablevision between the tractor and cart A at this instant?

Figure 6.8 (a) A complimentary-body diagram is shown, which indicates all the external forces on the system consisting of the tractor and luggage carts for carrying airline luggage. (b) A gratuitous-body diagram of the tractor only is shown isolated in order to calculate the tension in the cable to the carts.

Strategy

A free-trunk diagram shows the driving forcefulness of the tractor, which gives the organization its acceleration. Nosotros just need to consider movement in the horizontal direction. The vertical forces remainder each other and it is not necessary to consider them. For office b, nosotros make use of a gratis-body diagram of the tractor lonely to determine the force between it and cart A. This exposes the coupling force

which is our objective.

Solution

1. 

   and

   

   so

   

   Since dispatch is a office of time, we tin can make up one's mind the velocity of the tractor by using

   

   with the initial condition that

   

   at

   

   We integrate from

   

   to

   

   

2. Refer to the costless-body diagram in (Figure)(b).

   

Significance

Since the forcefulness varies with time, we must apply calculus to solve this trouble. Detect how the total mass of the system was of import in solving (Figure)(a), whereas simply the mass of the truck (since it supplied the force) was of utilize in (Effigy)(b).

Recall that

and

. If acceleration is a part of fourth dimension, nosotros can use the calculus forms developed in Motion Forth a Straight Line, as shown in this example. Nevertheless, sometimes acceleration is a part of deportation. In this case, we can derive an important result from these calculus relations. Solving for dt in each, we accept

and

Now, equating these expressions, we have

We can rearrange this to obtain

Example

Motion of a Projectile Fired Vertically

A 10.0-kg mortar shell is fired vertically upward from the footing, with an initial velocity of 50.0 chiliad/s (see (Effigy)). Determine the maximum superlative it volition travel if atmospheric resistance is measured as

where v is the speed at whatsoever instant.

Figure 6.9 (a) The mortar fires a trounce straight up; we consider the friction force provided by the air. (b) A complimentary-torso diagram is shown which indicates all the forces on the mortar trounce.

Strategy

The known strength on the mortar shell can be related to its dispatch using the equations of motion. Kinematics tin then be used to relate the mortar shell'south acceleration to its position.

Solution

Initially,

and

At the maximum height

The free-torso diagram shows

to human action downward, because it slows the upward motion of the mortar trounce. Thus, nosotros can write

The acceleration depends on 5 and is therefore variable. Since

nosotros tin relate a to 5 using the rearrangement described above,

We replace ds with dy because we are dealing with the vertical direction,

Nosotros now separate the variables (v's and dv'south on one side; dy on the other):

Thus,

Significance

Notice the need to employ calculus since the forcefulness is not constant, which also means that dispatch is not constant. To make matters worse, the force depends on v (not t), and so we must apply the fox explained prior to the example. The reply for the height indicates a lower elevation if there were air resistance. We will deal with the effects of air resistance and other drag forces in greater item in Drag Force and Concluding Speed.

Check Your Understanding

If atmospheric resistance is neglected, find the maximum height for the mortar shell. Is calculus required for this solution?

[reveal-answer q="fs-id1165036795612″]Show Solution[/reveal-respond]

[hidden-answer a="fs-id1165036795612″]

128 chiliad; no

[/hidden-respond]

Explore the forces at piece of work in this simulation when you try to push button a filing cabinet. Create an applied strength and see the resulting frictional force and total forcefulness acting on the cabinet. Charts show the forces, position, velocity, and acceleration vs. time. View a complimentary-body diagram of all the forces (including gravitational and normal forces).

Summary

• Newton's laws of motion can be applied in numerous situations to solve motion problems.
• Some problems contain multiple force vectors acting in different directions on an object. Exist sure to describe diagrams, resolve all forcefulness vectors into horizontal and vertical components, and describe a complimentary-body diagram. Always analyze the direction in which an object accelerates and so that you can decide whether

  

  or

  

• The normal force on an object is not always equal in magnitude to the weight of the object. If an object is accelerating vertically, the normal forcefulness is less than or greater than the weight of the object. Likewise, if the object is on an inclined plane, the normal force is always less than the full weight of the object.
• Some problems contain several concrete quantities, such equally forces, acceleration, velocity, or position. Y'all can use concepts from kinematics and dynamics to solve these problems.

Conceptual Questions

To simulate the credible weightlessness of space orbit, astronauts are trained in the concord of a cargo shipping that is accelerating downwards at thou. Why practise they appear to be weightless, as measured by standing on a bath scale, in this accelerated frame of reference? Is there any departure between their credible weightlessness in orbit and in the aircraft?

[reveal-answer q="fs-id1165037207907″]Bear witness Solution[/reveal-answer]

[hidden-respond a="fs-id1165037207907″]

The scale is in free fall forth with the astronauts, then the reading on the calibration would exist 0. At that place is no difference in the apparent weightlessness; in the shipping and in orbit, complimentary fall is occurring.

[/subconscious-answer]

Issues

A 30.0-kg girl in a swing is pushed to one side and held at rest by a horizontal force

and then that the swing ropes are

with respect to the vertical. (a) Summate the tension in each of the two ropes supporting the swing under these weather. (b) Summate the magnitude of

[reveal-answer q="fs-id1165037883543″]Evidence Solution[/reveal-answer]

[hidden-answer a="fs-id1165037883543″]

a. 170 N; b. 170 N

[/hidden-answer]

Find the tension in each of the three cables supporting the traffic calorie-free if it weighs 2.00 × 10² Due north.

Three forces deed on an object, considered to be a particle, which moves with constant velocity

Ii of the forces are

and

Observe the 3rd force.

[reveal-reply q="fs-id1165038107216″]Prove Solution[/reveal-answer]

[hidden-answer a="fs-id1165038107216″]

[/hidden-answer]

A flea jumps past exerting a strength of

directly down on the ground. A breeze bravado on the flea parallel to the ground exerts a force of

on the flea while the flea is nonetheless in contact with the ground. Find the direction and magnitude of the acceleration of the flea if its mass is

. Do not neglect the gravitational force.

Two muscles in the back of the leg pull upward on the Achilles tendon, as shown below. (These muscles are called the medial and lateral heads of the gastrocnemius muscle.) Observe the magnitude and direction of the full force on the Achilles tendon. What blazon of movement could exist acquired by this force?

[reveal-reply q="445142″]Show Solution[/reveal-respond]
[subconscious-reply a="445142″]376 Due north pointing up (along the dashed line in the figure); the strength is used to raise the heel of the foot.[/subconscious-answer]

Later on a mishap, a 76.0-kg circus performer clings to a trapeze, which is being pulled to the side past another circus artist, as shown here. Calculate the tension in the two ropes if the person is momentarily motionless. Include a costless-body diagram in your solution.

A 35.0-kg dolphin decelerates from 12.0 to 7.50 thousand/s in 2.30 s to bring together another dolphin in play. What average forcefulness was exerted to slow the first dolphin if it was moving horizontally? (The gravitational strength is balanced past the buoyant force of the water.)

[reveal-answer q="fs-id1165037017923″]Evidence Solution[/reveal-answer]

[hidden-answer a="fs-id1165037017923″]

−68.5 North

[/hidden-respond]

When starting a pes race, a 70.0-kg sprinter exerts an average forcefulness of 650 N astern on the ground for 0.800 s. (a) What is his last speed? (b) How far does he travel?

A large rocket has a mass of

at takeoff, and its engines produce a thrust of

(a) Notice its initial acceleration if information technology takes off vertically. (b) How long does it take to achieve a velocity of 120 km/h straight upwardly, assuming constant mass and thrust?

[reveal-answer q="fs-id1165037170393″]Show Solution[/reveal-answer]

[hidden-respond a="fs-id1165037170393″]

a.

; b. 4.33 s
[/hidden-answer]

A basketball game player jumps direct upwardly for a ball. To do this, he lowers his body 0.300 yard and so accelerates through this distance by forcefully straightening his legs. This player leaves the floor with a vertical velocity sufficient to carry him 0.900 m above the flooring. (a) Calculate his velocity when he leaves the flooring. (b) Calculate his dispatch while he is straightening his legs. He goes from nil to the velocity constitute in (a) in a distance of 0.300 m. (c) Calculate the force he exerts on the floor to practice this, given that his mass is 110.0 kg.

A 2.50-kg fireworks crush is fired directly up from a mortar and reaches a height of 110.0 yard. (a) Neglecting air resistance (a poor assumption, merely we volition brand it for this example), calculate the shell's velocity when it leaves the mortar. (b) The mortar itself is a tube 0.450 chiliad long. Calculate the average acceleration of the beat in the tube every bit it goes from nothing to the velocity found in (a). (c) What is the average force on the vanquish in the mortar? Express your respond in newtons and equally a ratio to the weight of the beat.

[reveal-reply q="fs-id1165037223045″]Show Solution[/reveal-reply]

[hidden-answer a="fs-id1165037223045″]

a. 46.4 k/southward; b.

c. 5.99 × 10³ Northward; ratio of 245
[/hidden-answer]

A 0.500-kg potato is fired at an angle of

above the horizontal from a PVC pipe used as a "murphy gun" and reaches a pinnacle of 110.0 k. (a) Neglecting air resistance, summate the spud's velocity when it leaves the gun. (b) The gun itself is a tube 0.450 m long. Summate the average acceleration of the irish potato in the tube every bit it goes from zero to the velocity institute in (a). (c) What is the average force on the murphy in the gun? Express your answer in newtons and every bit a ratio to the weight of the potato.

An elevator filled with passengers has a mass of

. (a) The elevator accelerates upwardly from rest at a rate of

for ane.50 s. Calculate the tension in the cable supporting the lift. (b) The elevator continues upwards at abiding velocity for 8.50 s. What is the tension in the cable during this time? (c) The elevator decelerates at a rate of

for 3.00 south. What is the tension in the cablevision during deceleration? (d) How high has the elevator moved above its original starting point, and what is its last velocity?

[reveal-respond q="fs-id1165038362269″]Show Solution[/reveal-reply]

[hidden-answer a="fs-id1165038362269″]

a.

b.

c.

d. 19.four m, 0 m/s
[/hidden-answer]

A twenty.0-g ball hangs from the roof of a freight auto past a string. When the freight auto begins to move, the string makes an angle of

with the vertical. (a) What is the acceleration of the freight machine? (b) What is the tension in the cord?

A student's backpack, full of textbooks, is hung from a spring scale attached to the ceiling of an elevator. When the elevator is accelerating downwardly at

, the scale reads 60 N. (a) What is the mass of the haversack? (b) What does the calibration read if the elevator moves upwards while slowing down at a rate

? (c) What does the scale read if the lift moves upward at constant velocity? (d) If the elevator had no brakes and the cable supporting information technology were to pause loose and so that the lift could fall freely, what would the spring scale read?

[reveal-answer q="fs-id1165034495684″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1165034495684″]

a. 10 kg; b. xc Northward; c. 98 North; d. 0

[/hidden-answer]

A service elevator takes a load of garbage, mass 10.0 kg, from a floor of a skyscraper under construction, down to ground level, accelerating downwards at a rate of

. Detect the magnitude of the force the garbage exerts on the floor of the service elevator?

A roller coaster car starts from rest at the top of a track thirty.0 m long and inclined at

to the horizontal. Assume that friction can be ignored. (a) What is the acceleration of the car? (b) How much time elapses earlier information technology reaches the lesser of the rails?

[reveal-respond q="fs-id1165038003888″]Bear witness Solution[/reveal-respond]

[hidden-answer a="fs-id1165038003888″]

a.

; b. 4.2 s
[/hidden-answer]

The device shown below is the Atwood's car considered in (Figure). Assuming that the masses of the string and the frictionless caster are negligible, (a) observe an equation for the acceleration of the ii blocks; (b) observe an equation for the tension in the string; and (c) find both the acceleration and tension when cake 1 has mass 2.00 kg and block 2 has mass four.00 kg.

2 blocks are connected by a massless rope as shown below. The mass of the cake on the table is 4.0 kg and the hanging mass is 1.0 kg. The table and the caster are frictionless. (a) Notice the acceleration of the system. (b) Find the tension in the rope. (c) Find the speed with which the hanging mass hits the flooring if it starts from balance and is initially located 1.0 one thousand from the floor.

[reveal-answer q="746415″]Testify Solution[/reveal-reply]
[hidden-reply a="746415″]a.

b. vii.8 N; c. 2.0 m/southward[/hidden-answer]

Shown below are 2 carts connected by a string that passes over a modest frictionless pulley. Each cart rolls freely with negligible friction. Calculate the acceleration of the carts and the tension in the cord.

A 2.00 kg block (mass ane) and a 4.00 kg block (mass 2) are continued by a light string as shown; the inclination of the ramp is

. Friction is negligible. What is (a) the acceleration of each block and (b) the tension in the string?

[reveal-answer q="709568″]Show Solution[/reveal-answer]
[hidden-answer a="709568″]a.

(mass ane accelerates upward the ramp as mass 2 falls with the aforementioned acceleration); b. 21.five N[/hidden-respond]

fordwisford.blogspot.com

Source: https://opentextbc.ca/universityphysicsv1openstax/chapter/6-1-solving-problems-with-newtons-laws/

Share this post